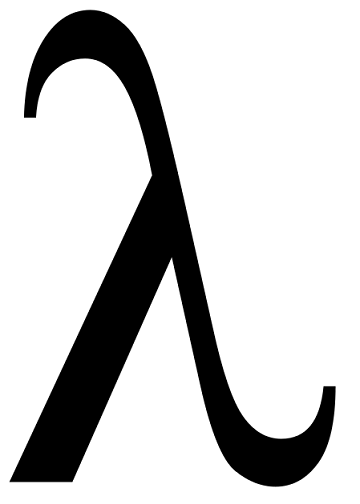In simple terms, $\lambda$-calculus is a way to specify function applications without actually defining their names. Normally in programming, we can define a function like so:

let f(x) = x * x + 1 in B

where B is a command. This defines what f does, given some variable x that’s bound to the function body, x * x + 1. Equivalently, we can denote this binding of x:

The “function declaration” in the above statement, $\lambda x. x * x + 1$ is called a lambda expression or an abstraction, which is saying “when this is applied to some $x$, it returns $x \times x + 1$”. Note that a lambda expression/abstraction doesn’t give notions on what $x$ is. The only thing it implies is the relationship between some operand $x$ and operator $x \times x + 1$.

Note that abstractions are not functions!! Abstractions can be used to denote a function application, but doesn’t always define a function by itself.

This is why unnamed functions in typical programming languages are called lambda functions, because a lambda function yields some value defined by relationships between its arguments and the function body. Hence it’s an “unnamed function”.

Suppose lambda expressions didn’t exist. All function calls must be declared with let terms. For example, say we wanted to calculate $\int_0^1 x^2 + 1$ with a defined integration function integrate(lb, ub, f). This can be written as:

But with lambda expressions, this gets simplified into:

the $\lambda$-calculus we will be looking at in this chapter only works with untyped $\lambda$-calculus. This means we don’t consider the types of variables and expressions. Untyped $\lambda$-calculus is simpler to describe, but isn’t sufficient in describing mathematical logic. We need typed $\lambda$-calculus as a stronger tool.

Syntax and Basic Rules

$\lambda$-calculus is composed of expressions called $\lambda$-terms. We will define the set of all lambda terms $E$, inductively, like from formal logic:

1. A term of form $x$, where $x$ is in some set of variables $V$, denotes a variable.
2. A term of form $\lambda x. E$, is called a lambda expression or to reduce confusion, also called an abstraction.
3. A term of form $E_0 \ E_1$ is called application of $E_0$ to $E_1$. Equivalently, we see $E_0$ as the operator and $E_1$ as operand.

Application is left associative, meaning

and in abstractions bounded variables are bound to the closest binder, meaning:

$\alpha$-Conversion

Since every abstraction $\lambda x. E$ binds some variable $x$ in scope $E$. We need to identify the set of free variables that’s allowed in an expression. The set $\text{FV}(E)$ of free variables in expression E is defined as:

So free variable are variables which are usused within a lambda abstraction. In standard programming terms, you can think of it as variables which aren’t bounded by some scope.

Once we identifed the set of free variables in an expression $E$, we can try and substitute all free variables in $E$ with another expression. Let $E/\delta$ denote substituting occurences of variable $x$ in $E$, with $\delta \ x$. $E/\delta$ is defined as:

where

Let’s go through this step by step:

1. If the expression $E$ is just a variable($x$) we can just replace $x$ with $\delta$ applied to $x$, $\delta \ x$
2. If $E$ is an application, we first perform substitution on both operator and operands: $(E_0 / \delta)$ and $(E_1 / \delta)$. And finally we just apply the substituted operator to the substituted operand.
3. If $E$ is an abstraction , $x$ is not a free variable. So we cannot just substitute $\delta \ x$. Instead, we can rename $x$ into some other variable $x_{new}$, and then perform substitution on $x_{new}$. However, if we were to change $x$ into some variable that’s being used inside E, this can change the meaning of the abstraction. For example, suppose we have $\lambda x. y \ x$. It will always return some variable $y$, regardless of x. But if you changed the bounded variable $x$ to $y$: $\lambda y. y \ x$, it now becomes the identity function. When we are substituting variables in an abstraction, we are free to change the bound variable $x$ to $x_{new}$, given that the new variable $x_{new}$ isn’t being used in the abstraction. This is equivalent to $x_{new} \notin \bigcup_{\omega \in \text{FV}(E) - {x}} \text{FV}(\delta \ \omega)$, since free variables are variables being used inside the terms.

Applying the substitution rule to $\lambda x. E$, resulting in $\lambda x_{new}. (E/x \rightarrow x_{new})$ is called renaming. And if some expression $E’$ is obtained after applying multiple renamings to $E$, we say that $E$ and $E’$ are $\alpha$-equivalent. Then, it can be shown that:

This is simply because all we have done were renaming bound variables to some other variable, that’s not being used with the expression. In code form, we can see that

def my_function(a, b):
	return a + b + c  # c is some other variable

and

def my_function(renamed_a, renamed_b):
	return renamed_a + renamed_b + c  # c is some other variable

are functionally equivalent.

Reduction

$\beta$-Reduction

Recall that $\lambda$-calculus is just a way to represent repeated function applications. This leads us to thinking, if we compose applications, couldn’t we reduce them so that we can sequentially apply the function? The answer to this is yes. Consider the following lambda term:

A term of this form is called a redex, which represents applying the function $(\lambda x. E)$ to the argument $E’$. This means $(\lambda x. E)$ should yield the value of $E$ when $x$ in $E$ denotes the value of $E’$. In other words, we substitute $E’$ for $x$ in $E$.

Suppose we have an expression $E_0$ that contains one or more occurences of $(\lambda x. E) E’$. Let $E_1$ be obtained from $E_0$ by replacing $(\lambda x. E) E’$ with $E/x \rightarrow E’$. Then we write $E_0 \rightarrow E_1$, and say that $E_0$ contracts to $E_1$. Using this notation, we can write the $\beta$-reduction rule:

This is a very intuitive rule - we can convert function applications by just substituting function calls with its function body applied to the arguments.

The following rules also hold: Renaming:

Contextual Closure

\(\frac{E_0 \rightarrow E_1}{E_0' \rightarrow E_1'}\) where $E_1’$ is obtained from $E_0’$ by replacing one occurence of $E_0$ in $E_0’$ in $E_1$

If $E_1’$ is obtained from $E$ by zero or more contractions, then we say $E$ reduces to $E’$ and write that as $E \rightarrow^* E’$. From this we can derive more rules:

Transitive and Reflexive Closure

For an expression, we can continuously apply $\beta$-reduction (and $\alpha$-conversion if needed) until no redexes exist in the expression. Thus at a certain point we can no longer apply $\beta$-reduction, reaching a terminal state. This type of terminal expression is called a normal form, and say that “$E’$ is a normal form of $E$”, if $E$ reduces to normal form $E’$.

As an example, let’s try reducing $(\lambda x. (\lambda y. y \ x)z)(z \ w)$:

However, if we perform $(\lambda y. y \ x)z/x \rightarrow (z \ w)$ first, we get a different order of reduction:

but end up with the same normal form, $z \ (z \ w)$.

This is the Church-Rosser Theorem, which states that the order of reduction does not matter. More formally, if $a \rightarrow^* b$ and $a \rightarrow^* c$, then there exists some $d$ such that $b \rightarrow^* d$ and $c \rightarrow^* d$. ![[church_rosser.png]]

$\eta$-Reduction

$\eta$-reduction expresses the notion of functional extensionality:

Regardless of the form of $e$ and the input $v$, the abstraction $\lambda v. ev$ always contracts to e. No matter how many “identity” functions are applied to $e$, for all inputs the resulting normal form is always the same.

Why does $v$ need not be a free variable in $e$? Functional extensionality implies:

Notice that the argument $x$ is same across the two functions. Suppose I wish to encode it in lambda calculus. I can define some function g as:

If $x$ is not a free variable in $f$, which by definition, implies that $x$ is indeed the argument of $f$ we immediately can identify functional extensionality as implied by the same argument being passed to f and g.

Suppose I instead use $x’ \in FV(f)$. $g = \lambda x’. f x’$ doesn’t immediately reveal that $x’ = x$ so the only choice is to perform an $\beta$-reduction which substitutes $x’$ in place of $x$.

Church-Turing Thesis and the Church Numerals

From wikipedia:

In computability theory, the Church–Turing thesis (also known as computability thesis, the Turing–Church thesis, the Church–Turing conjecture, Church’s thesis, Church’s conjecture, and Turing’s thesis) is a thesis about the nature of computable functions. It states that a function on the natural numbers can be calculated by an effective method if and only if it is computable by a Turing machine.

Church shows that indeed natural numbers and arithmetic are representable solely with $\lambda$-calculus, proving that $\lambda$-calculus is turing-complete. The representation of the natural numbers with $\lambda$-terms, is called the Church Numerals. In fact, you can represent any arbitrary data type and calculations involving them in $\lambda$-calculus, including, but not limited to integers, finite-precision real numbers, booleans, arrays, and so on. This is the Church-Turing thesis.

Note: this section is for those who have keen curiosity as to what $\lambda$-calculus can and cannot represent. You may skip this section if you don’t want to read it.

The key idea is to represent natural numbers, and their succesive numbers as a self-composite(recursive) function that “does something”:

![[church_numerals_composition.svg]]

For any $n \in \mathbb{N}$, define $f^n(x)$ as the following:

Then, for any $n \in \mathbb{N}$, the $n$th Church Numeral $c_n$ is the $\lambda$-term

You might look at this and ask, “so where is the number $n$?”. This may sound confusing, but the Church Numerals does not mean to return an output number $n$. Instead, it holds the meaning of applying some function $f$, to some argument $x$, $n$ times. Thus this function form itself is the Church Numeral, not its result. It implys, “do something $n$ amount of times”.

If we plug in the successor function $S$ as $f$ and zero for $x$, then we have the peano numerals: